A 3D STOCHASTIC MODEL FOR GEOMETRICAL CHARACTERIZATION OF PARTICLES IN TWO-PHASE FLOW APPLICATIONS
DOI:
https://doi.org/10.5566/ias.1942Keywords:
3D modeling, finite point process, Matérn point process, stochastic geometry, particles size distribution, two-phase flowAbstract
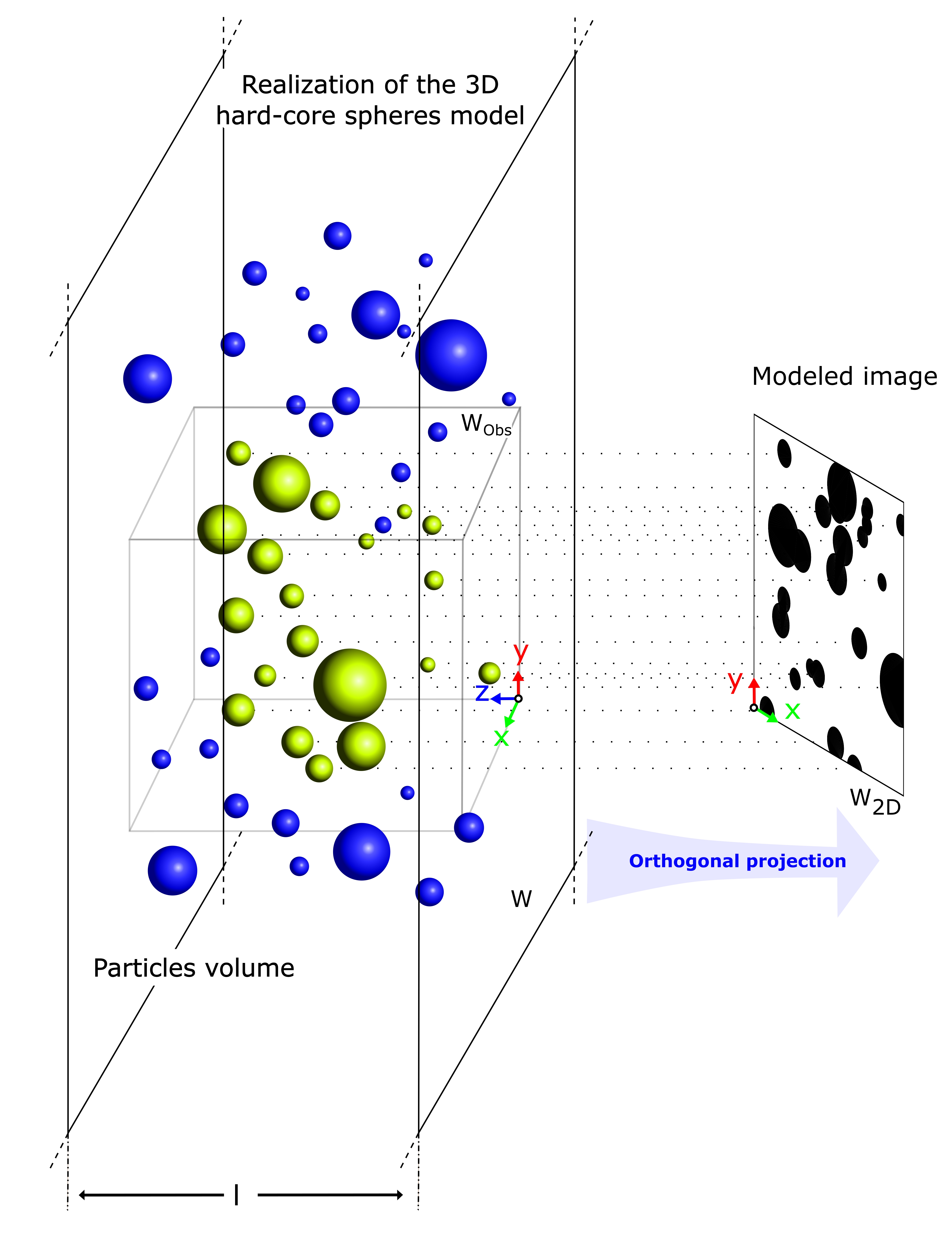
In this paper a new approach to geometrically model and characterize 2D silhouette images of two-phase flows is proposed. The method consists of a 3D modeling of the particles population based on some morphological and interaction assumptions. It includes the following steps. First, the main analytical properties of the proposed model – which is an adaptation of the Matérn type II model – are assessed, namely the effect of the thinning procedures on the population’s fundamental properties. Then, orthogonal projections of the model realizations are made to obtain 2D modeled images. The inference technique we propose and implement to determine the model parameters is a two-step numerical procedure: after a first guess of the parameters is defined, an optimization procedure is achieved to find the local minimum closest to the constructed initial solution. The method was validated on synthetic images, which has highlighted the efficiency of the proposed calibration procedure. Finally, the model was used to analyze real, i.e., experimentally acquired, silhouette images of calibrated polymethyl methacrylate (PMMA) particles. The population properties are correctly evaluated, even when suspensions of concentrated monodispersed and bidispersed particles are considered, hence highlighting the method’s relevance to describe the typical configurations encountered in bubbly flows and emulsions.
References
Audet C, Dennis JE (2002). Analysis of generalized pattern searches. SIAM J Optimiz 13:889–903.
Arns CH, Knackstedt MA, Mecke KR (2003). Reconstructing complex materials via effective grain shapes. Phys Rev Lett 91:215506.
Baddeley A, Jensen EBV (2004). Stereology for statisticians. New York: Chapman & Hall/CRC.
Biswal B, Øren P E, Held R J, Bakke S, Hilfer R (2011). Modeling of multiscale porous media. Image Anal Stereol 28:23–34. 246 Image Anal Stereol 2018;37:233-247
Chiu SN, Stoyan D, Kendall W, Mecke J (2013). Stochastic geometry and its applications, 3rd Ed. Chichester: Wiley.
Daley DJ, Vere-Jones D (2003). An introduction to the theory of point processes. Vol I: Elementary theory and methods. New York: Springer.
Davidon WC (1991). Variable metric method for minimization. SIAM J Optimiz 1:1–17. de Langlard M, Al-Saddik H, Charton S, Debayle J,
Lamadie F (2018). An efficiency improved recognition algorithm for highly overlapping ellipses: application to dense bubbly flows. Pattern Recogn Lett 101:88–95.
Dereudre D, Lavancier F, Helisov´a K (2014). Estimation of the intensity parameter of the germ-grain Quermassinteraction model when the number of germs is not observed. Scand J Stat 41:809–29.
Descombes X (2011). Application de la g´eom´etrie stochastique `a l’analyse d’images. Paris: Herm`es- Lavoisier.
Diggle P (1981). Binary mosaics and the spatial pattern of heather. Biometrics 37:531–9. Emery X, Kracht W, Egana A (2012). Using two-point set statistics to estimate the diameter distribution in Boolean models with circular grains. Math Geosci 44:805–22.
Hall P (1985). Counting methods for inference in binary mosaics. Biometrics 41:1049–52. Illian J, Penttinen A, Stoyan H, Stoyan D (2008). Statistical analysis and modelling of spatial point patterns.
Chichester: Wiley. Kracht W, Emery X, Paredes C (2013). A stochastic approach for measuring bubble size distribution via image analysis. Int J Miner Process 121:6–11.
Kubınova L, Radochov´a B, Lhot´akov´a Z, Kubinov´a Z, Albrechtov´a J (2017). Stereology, and unbiased methodological approach to study plant anatomy and cytology: past, present and future. Image Anal Stereol 36:187–205.
Lau YM, Deen NG, Kuipers JAM (2013). Development of an image measurement technique for size distribution in dense bubbly flows. Chem Eng Sci 94:20–9.
Maaß S, Wollny S, Voigt A, Kraume M (2011). Experimental comparison of measurement techniques for drop size distributions in liquid/liquid dispersions. Exp Fluids 50:259–69.
Mansson M, Rudemo M (1960). Random patterns of nonoverlapping convex grains. Adv Appl Probab 34:718–38.
Matern B (1960). Spatial variation: stochastic models and their application to some problems in forest surveys and other sampling investigations. Statens skogsforskningsinstitut.
Matheron G (1972). Ensembles al´etoires et g´eom´etrie int´egrale. Les cahiers du centre de morphologie math´ematiques de Fontainebleau. Mrkviˇcka T, Rataj J (2009). On estimation of intrinsic volume densities of stationary random closed sets via parallel sets in the plane. Kybernetika 45:931–45.
Mrkvicka T (2009). On testing of general random closed set model hypothesis. Kybernetika 45:293–308.
Mrkvicka T, Mattfeldt T (2011). Testing histological images of mammary tissues on compatibility with the boolean model of random sets. Image Anal Stereol 30:11–8.
Muthukannan K, Latha P (2015). A PSO model for disease pattern detection on leaf surfaces. Image Anal Stereol 34:209–16.
Nagata T (2000). Three-dimensional observations on thick biological specimens by high voltage electron microscopy. Image Anal Stereol 19:51–6.
Ohser J, Schladitz K (2009). 3D images of materials structures: processing and analysis. Weinheim: Wiley VCH.
Stoyan D, Stoyan H (1985). On one of Mat´ern’s hardcore point process models. Math Nachr 122:205–14.
Teichmann J, Ballani F, van den Boogaart K.G (2013). Generalizations of Matern hard-core point processes. Spat Stat 3:33–53.
Weil W (1988). Expectation formulas and isoperimetric properties for non-isotropic Boolean models. J Microsc 151:235–45.
Zafari S, Eerola T, Sampo J (2015). Segmentation of overlapping elliptical objects in silhouette images. IEEE T Image Process 24:5942–52.
Downloads
Published
Issue
Section
License
Copyright (c) 2018 Image Analysis & Stereology

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.









